LoSiA: Efficient High-Rank Fine-Tuning via Subnet Localization and Optimization

Posted Oct 20, 2025

By Seokgi Lee

13 min read

2025 EMNLP Oral Written By. Xujia Wang, Yunjia Qi, Bin Xu

개요

LoSiA는 고순위(high-rank) 파라미터 업데이트를 수행하면서도 낮은 계산 비용과 낮은 메모리 사용량을 유지하는 서브넷 기반 미세조정 방법
핵심 아이디어는 전체 모델이 아닌, gradient sparsity를 기반으로 가장 중요한 subnet을 동적으로 찾아내고 해당 부분만 학습하는 것

배경 및 문제의식

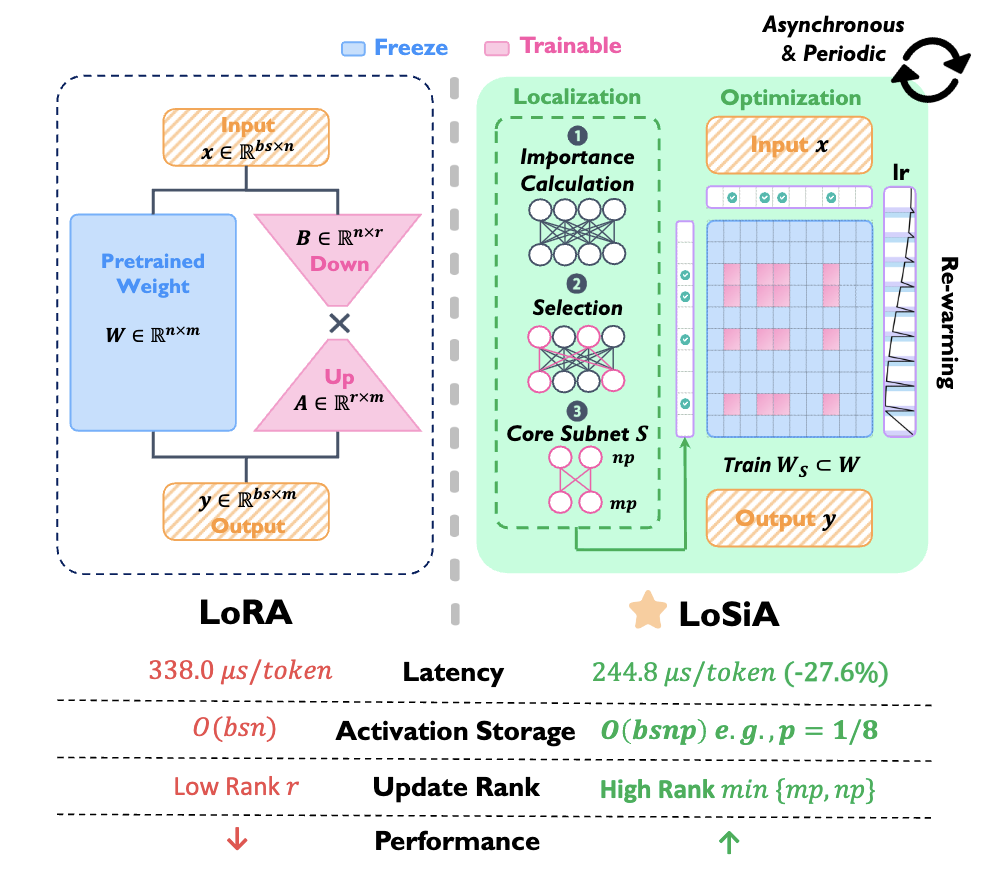
기존 LoRA는 다음과 같은 형태로 low-rank 업데이트를 수행:

\[\Delta W = BA, \quad \text{where } B \in \mathbb{R}^{n \times r}, A \in \mathbb{R}^{r \times m}, r \ll \min(n, m)\]

하지만 이 방식은:

도메인 특화 작업에서 underfitting 문제
matrix multiplication 오버헤드
저효율적 학습 구조

라는 한계가 존재.

제안 방법: LoSiA

1. Gradient 기반 서브넷 정의

모델 $f_0$ 의 파라미터 W, 데이터셋 $D = {B_i}{i=1}^N$, 각 배치 $B_i = {(x_j, y_j)}{j=1}^M$
서브넷은 다음과 같이 정의:
\[S = (X_S, Y_S, W_{X_S,Y_S})\]
- $X_S$: 입력 뉴런 집합
- $Y_S$: 출력 뉴런 집합
- $W_{X_S,Y_S}$: 연결된 weight

2. Gradient 기반 에러 상한 (SGD)

두 모델 $f_k$, $f_k’$ (하나는 전체 파라미터, 다른 하나는 서브넷만 학습) 사이의 MSE는 다음과 같은 upper bound를 가짐:
- 이 식은 중요한 gradient를 가지는 weight만 남기면 학습 성능이 보장됨을 이론적으로 설명.

\[L_{MSE} \leq \frac{\eta^2}{M} \|1_{(i,j)\notin P} \cdot \nabla_W L(B_k)\|_F^2 \|x\|_F^2\]

도출 과정
- 목적:
  전체 weight W 대신 일부 파라미터 $P \subset W$ 만 학습했을 때, 손실이 얼마나 증가하는지 예측

MSE 정의부터 시작
- 두 모델 f (전체 weight 학습) vs f’ (부분 weight 학습)의 출력 차이에 대한 평균제곱오차:
\[L_{\text{MSE}} = \frac{1}{M} \|y - y'\|_F^2 = \frac{1}{M} \|W x - W' x\|_F^2 = \frac{1}{M} \|(W - W') x\|_F^2\]
SGD에서 weight 업데이트
\[W' = W - \eta \cdot 1_{(i,j) \in P} \cdot \nabla_W L(B) \\ W - W' = \eta \cdot 1_{(i,j) \in P} \cdot \nabla_W L(B)\]
- 하지만 선택 안 된 weight가 성능에 미치는 영향을 보고 싶으므로:
  \[W - W' = -\eta \cdot 1_{(i,j) \notin P} \cdot \nabla_W L(B)\]
이걸 MSE에 대입
\[L_{\text{MSE}} = \frac{1}{M} \|(W - W') x\|_F^2 = \frac{1}{M} \|-\eta \cdot 1_{(i,j)\notin P} \cdot \nabla_W L(B) \cdot x\|_F^2 \\ = \frac{\eta^2}{M} \left\|1_{(i,j)\notin P} \cdot \nabla_W L(B)\right\|_F^2 \cdot \|x\|_F^2\]

결론
- 전체 weight 중 우리가 선택하지 않은 부분에 gradient가 많으면 → 모델이 성능을 잃을 위험이 크다
- 따라서, gradient가 큰 weight들을 최대한 많이 포함하는 게 좋다 → 서브넷 선택 기준으로 삼자

3. Parameter Importance 계산

LoSiA는 아래와 같은 식으로 중요도를 계산:

\[I = \left| \frac{\partial L}{\partial W_k} W_k - \frac{1}{2} W_k H_{kk} W_k \right|\]

즉, gradient가 큰 weight = 중요한 weight 라고 간주
- SGD에서의 weight 업데이트는: $W \leftarrow W - \eta \cdot \nabla_W L$
  - $\nabla_W L$: 손실 함수 LLL을 weight W로 미분한 gradient
  - $\eta$: learning rate
  - 즉, gradient가 크다는 것 = 그 weight가 loss를 줄이는데 큰 영향을 미친다는 것

이를 실시간 적용하기 위해 EMA 기반으로 다음과 같이 근사:

\[I_i(W_k) = \beta_1 I_{i-1}(W_k) + (1 - \beta_1) I(W_k)\] \[U_i(W_k) = \beta_2 U_{i-1}(W_k) + (1 - \beta_2) |\Delta I(W_k)|\]

최종 점수:

\[s(W_k) = I(W_k) \cdot U(W_k)\]

4. Subnet Localization 알고리즘

서브넷 선택은 NP-Hard 문제이며, 논문은 Greedy 기반 알고리즘을 사용:
- 상위 $\lfloor np \rfloor$개의 입력 뉴런 선택
- 해당 입력 기준으로 상위 $\lfloor mp \rfloor$개 출력 뉴런 선택
- 이 과정을 통해 중요한 서브넷 $S = (X_S, Y_S, W_{X_S, Y_S})$ 을 추출.
이 과정을 모든 레이어마다 반복하여 서브넷 선정
- Asynchronous Periodic Localization
  - 모든 layer가 동시에 subnet을 갱신하지 않고, 각 layer별로 주기 T 마다 비동기로 갱신
  예: 6개의 디코더 layer가 있으면,
  - Step 0–100: Layer 0의 중요도 계산 + subnet 선택
  - Step 100–200: Layer 1 → 이 때 Layer 0은 Freeze
  - … 반복
- 학습률도 재조정 (“Rewarming”)
  - 서브넷을 갱신한 layer는 짧은 warm-up을 다시 줘서 안정성 확보
    \[lr(t) = \left(\frac{t - t_0}{T}\right) \cdot lr \quad \text{(rewarming phase)}\]
  - 서브넷을 바꾸면 완전히 새로운 파라미터 집합을 훈련하게 됨
  - 갑자기 큰 learning rate로 훈련하면 gradient 폭주 가능
  - Rewarming을 통해 학습률을 부드럽게 시작 → 안정적 학습 가능
  - 서브넷이 바뀌었을 때 학습률 폭발 방지

5. 학습 최적화 및 LoSiA-Pro

LoSiA-Pro가 왜 필요한가?
- 기본 LoSiA도 서브넷만 골라서 학습하는 구조라 매우 효율적이지만,
- 여전히 두 가지 문제 존재:
  - (1) gradient 계산이 비효율적
    - 파라미터 일부만 학습하는데도
    - 여전히 전체 gradient 계산해야 하는 경우가 많음
  - (2) activation 저장 비용 큼
    - 학습 시 gradient 계산을 위해 forward의 입력값 x 를 저장해야 함
    - 하지만 입력 전체 $x \in \mathbb{R}^{n \times bs}$ 를 저장하는 건 부담이 큼
LoSiA-Pro는 학습 중 필요한 gradient 계산을 아래와 같이 분해:

\[\frac{\partial L}{\partial W_S} = x^T_{X_S} \cdot \frac{\partial L}{\partial y}_{Y_S}\]

이를 통해 gradient 계산 비용을 $O(nmbs) \to O(nmbsp^2)$로 줄임.
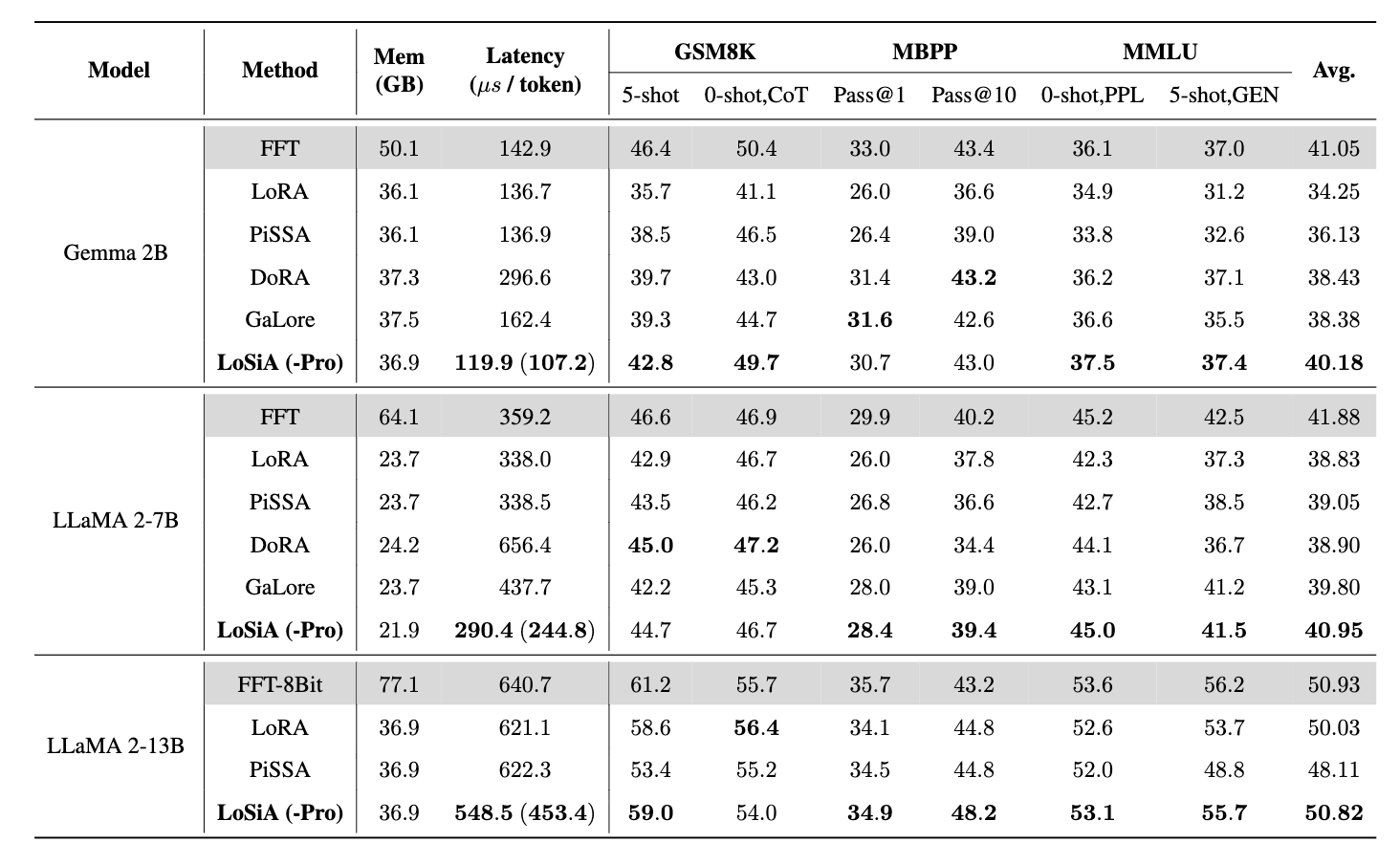
결과적으로 LoSiA-Pro는 LoRA 대비 약 27.6%의 latency 감소, 최대 13.4GB의 GPU 메모리 절약.

실험

사용된 모델

LLaMA-2 7B (주 실험용)
일부 실험에서 Gemman-2B, LLaMA-2 13B 도 사용

평가한 데이터셋 (총 9개)

MMLU (다중 분야 문답 평가), reasoning 중심 task
GSM8K (초등 수준 수학 문제), reasoning 중심 task
HumanEval (코딩 문제), reasoning 중심 task
BBH (Big Bench Hard, 고난이도 문제셋), reasoning 중심 task
ARC-C (과학, 수학, 논리)
HellaSwag (상식 기반 선택형)
TruthfulQA (허위 정보 판단)
Winogrande (공통 상식 + 언어)
PIQA (물리 기반 질문)

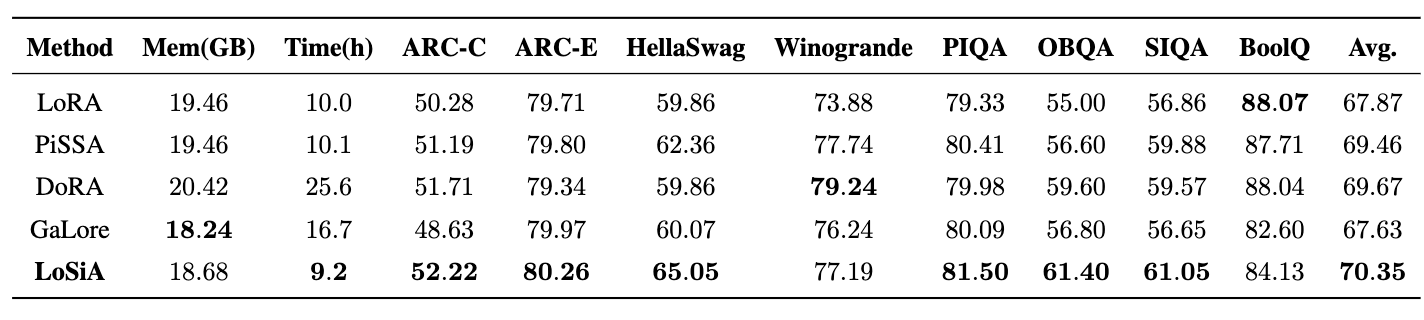
성능 비교

다른 LoRA 방법보다 높은 성능 및 추론 속도

LoSiA는 LLaMA-2 7B 모델을 사용한 상식 추론 태스크에서 다른 주요 PEFT 방법들 대비 가장 적은 학습 시간으로 가장 높은 전반적인 성능(평균 정확도)을 달성

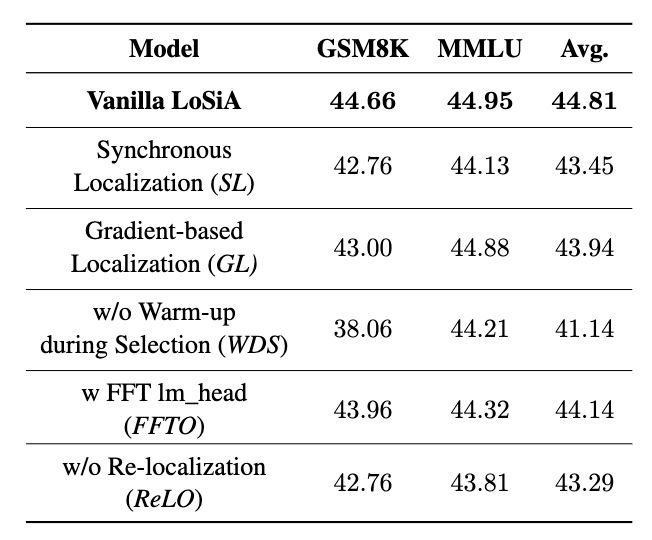
Ablation 실험

다양한 구성 요소들이 전체 성능에 미치는 영향을 분석하기 위한 Ablation Study 결과

LLaMA-2 7B 모델을 MetaMathQA 데이터셋으로 훈련하고 GSM8K 벤치마크에서 평가한 결과
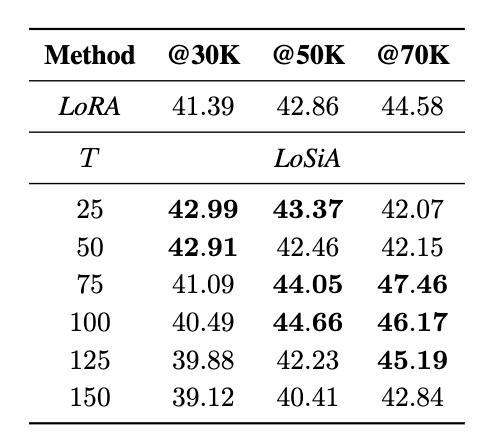
T 값과 데이터 규모의 상관관계:
- 표를 보면, 데이터셋 크기가 커질수록 최적의 T 값도 증가하는 경향
- @30K에서는 작은 T 값(25, 50)이 좋았고, @50K에서는 중간 T 값(75, 100), @70K에서는 더 큰 T 값(75, 100, 125)이 좋은 성능
- 논문에서는 “최적의 시간 슬롯 T는 훈련 세트의 크기와 양의 상관관계가 있다”고 언급

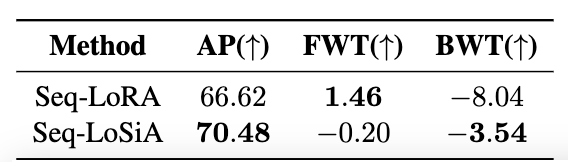
LoRA와 LoSiA를 Continual Learning 시퀀스에 적용했을 때의 성능을 비교
AP (Average Performance):
- 정의: 모델이 여러 작업을 순차적으로 학습한 후, 모든 학습된 작업에 대해 달성한 평균 정확도
  - $AP = \frac{1}{N} \sum_{i=1}^{N} P_{N,i}$
  - N: 총 학습된 작업의 수
  - $P_{N,i}$: 모든 N개 작업을 순차적으로 학습한 후, 특정 작업 i에 대한 모델의 성능 (정확도)
- 의미: 이 지표는 모델의 전반적인 학습 능력과 다양한 작업을 수행하는 능력을 측정하며, 값이 높을수록 전반적인 성능이 우수함을 의미
FWT (Forward Transfer):
- 정의: 이전에 학습한 지식이 새로운 작업을 학습하는 데 얼마나 긍정적인 영향을 미치는지(즉, 지식 전이가 얼마나 잘 일어나는지)를 측정하는 지표
  - $FWT = \frac{1}{N} \sum_{i=1}^{N} (P_{i,i} - P_{0,i})$
  - N: 총 학습된 작업의 수
  - $P_{i,i}$: 작업 i까지 순차적으로 학습한 후, 작업 i에 대한 모델의 성능
  - $P_{0,i}$: 작업 i만 독립적으로(즉, 이전 작업의 지식 없이) 학습했을 때의 모델 성능
- 의미: 값이 높을수록 이전 작업에서 얻은 지식이 새로운 작업 학습에 더 도움이 되었음을 의미. 음수 값은 오히려 부정적인 전이가 발생했음을 나타냄.
BWT (Backward Transfer):
- 정의: 새로운 작업을 학습할 때 이전에 학습했던 작업에 대한 지식을 얼마나 잊어버리는지(망각 현상)를 측정하는 지표.
  - $BWT = \frac{1}{N-1} \sum_{i=1}^{N-1} (P_{N,i} - P_{i,i})$
  - N: 총 학습된 작업의 수
  - $P_{N,i}$: 모든 N개 작업을 순차적으로 학습한 후, 특정 작업 i에 대한 모델의 성능
  - $P_{i,i}$: 작업 i를 학습한 직후, 작업 i에 대한 모델의 성능 (즉, 작업 i에 대한 최종 학습 상태)
- 의미: 음수 값은 망각이 발생했음을 의미하며, 0에 가까울수록 망각이 적고 이전 지식이 더 잘 보존되었음을 나타냄. 양수 값은 이전 작업에 대한 성능이 향상되었음을 의미.
LoSiA의 핵심 아이디어인 동적인 서브 네트워크 선택 및 최적화가 모델의 지식 보존에 긍정적인 영향을 미친다는 논문의 주장을 뒷받침.

결론

LoSiA는 고효율, 고성능의 PEFT 프레임워크로,
- Gradient 기반 중요도 계산
- 동적 subnet 선택
- LoSiA-Pro 통한 가속화
한계
- multi-tasking이나 비언어 도메인(예: Vision)에 대한 일반화는 아직 미검증 상태.

Paper

LLM PEFT

This post is licensed under CC BY 4.0 by the author.