MetaEmbed: Scaling Multimodal Retrieval at Test-Time with Flexible Late Interaction
Written By. Zilin Xiao, Qi Ma, Mengting Gu
1. 문제 정의
멀티모달 검색의 기본 접근의 병목: “표현력 vs 효율” 트레이드오프
(A) Single-vector 임베딩
쿼리/후보를 각각 “하나의 벡터”로 압축하면 인덱스/서치가 매우 효율적이지만, 멀티모달에서 중요한 fine-grained(세부) 정보가 손실되어 표현력이 제한된다는 문제.
(B) 멀티 벡터(Multi-vector) + late interaction(ColBERT류)
토큰/패치 단위로 다수 벡터를 유지하고 late interaction(예: MaxSim)으로 점수화하면 표현력은 크게 좋아지지만,
- 인덱스가 커지고
- 점수 계산이 느려지고
- 특히 “쿼리도 이미지, 후보도 이미지” 같은 multimodal-to-multimodal에서 토큰 수가 양쪽 모두 커 코스트가 너무 많이 듬.
따라서 논문은 multi-vector의 표현력은 유지하되, 벡터 개수는 아주 작게 가져가면서, 동시에 테스트 시점에 성능-비용을 유연하게 조절(test-time scaling) 가능한 프레임워크를 목표로 함.
2. MetaEmbed
- Meta Tokens로 “작은 개수의 멀티벡터” 만들기
- Matryoshka Multi-Vector Retrieval(MMR)로 “벡터들을 coarse→fine로 정렬”시키는 학습 방법
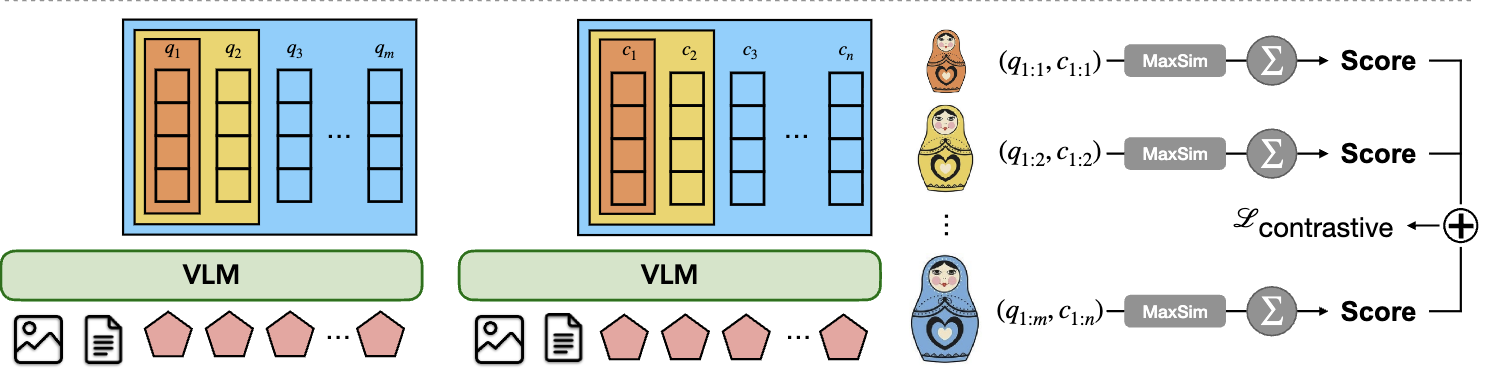
2.1 Late Interaction(ColBERT 스타일)
먼저 논문은 late interaction을 전제로.
- 쿼리 임베딩 행렬 $E_q \in \mathbb{R}^{N_q \times D}$
- 후보 임베딩 행렬 $E_d \in \mathbb{R}^{N_d \times D}$
late interaction 점수는
- 각 쿼리 벡터 $E_q^{(i)}$마다 후보 벡터들 중 가장 유사한 것의 점수(MaxSim) 를 취한 뒤
- 그 값을 쿼리 벡터들에 대해 합산
이 방식은 “토큰 단위로 align”이 가능해서 single-vector보다 표현력이 좋지만, 문제는 $N_q, N_d$가 커지면 계산/인덱스가 매우 커짐.
2.2 Meta Tokens로 벡터 수를 고정·축소
(1) 아이디어
토큰/패치 임베딩을 그대로 쓰지 않고, 입력 시퀀스 뒤에 학습 가능한 Meta Tokens를 “고정 개수”로 넣기.
그리고 VLM이 이를 함께 처리한 뒤, 마지막 레이어에서 Meta Tokens 위치의 hidden state들만 뽑아 multi-vector 임베딩으로 사용.
- 수백 개 패치 벡터 대신
- 후보 64개, 쿼리 16개 같은 작고 고정된 벡터 세트만 retrieval에 쓰는 구조.
(2) 입력/모델 수식 구조
VLM 파라미터를 $\theta$라 하고, 텍스트 토큰을 $x=[x_1,\dots,x_n],$ 이미지 입력을 I라고 할 때, 입력은 다음을 concat한 시퀀스:
- v: 시각(이미지) 토큰들
- t: 텍스트 토큰들
- $M_q \in \mathbb{R}^{R_q \times D}$: 쿼리용 Meta Tokens (학습)
- $M_c \in \mathbb{R}^{R_c \times D}$: 후보용 Meta Tokens (학습)
마지막 레이어 hidden states는
\[H = F_\theta(z^{(0)}) \in \mathbb{R}^{(P+n+R_q+R_c)\times D}\]여기서 Meta Token 위치의 hidden state만 뽑아서 쿼리/후보 임베딩으로 사용하기:
- $E^{(q)}_{meta} \in \mathbb{R}^{R_q \times D}$
- $E^{(c)}_{meta} \in \mathbb{R}^{R_c \times D}$
그리고 L2 정규화를 적용.
Meta Tokens는 “입력 내용을 압축해서 담는 learnable 슬롯(slot)들”처럼 동작 원래 토큰/패치 전체를 저장하지 않고, 소수 슬롯에 fine-grained 정보를 ‘요약’시키는 방향.
(3) retrieval score (Meta Tokens 기반 late interaction)
Meta Embeddings를 쓰면 late interaction 점수는
\[s(q,c) = \sum_{i=1}^{R_q} \max_{j\in[1,R_c]} \langle E_q^{(i)}, E_c^{(j)} \rangle\]여기서 핵심은 $R_q, R_c$가 매우 작게 고정되어 기존과 다르게 computation cost가 줄어들게됨
- 인덱스 크기: $O(N \cdot R_c \cdot D)$
- 쿼리-후보 스코어링: $O(R_q \cdot R_c \cdot D)$
2.3 MMR(Matryoshka Multi-Vector Retrieval)로 coarse→fine 계층화
Meta Tokens만 붙인다고 해서 테스트 시점에 벡터 수를 줄여도 성능이 유지되지는 않음.
따라서, 논문은 마트료시카 학습을 추가.
(1) 그룹 정의: prefix-nested 그룹들
쿼리/후보 각각에 대해 G개의 prefix 길이 정의 → 각 그룹이 마트료시카 차원 역할.
- 쿼리: $1 \le r_q^{(1)} < r_q^{(2)} < \dots < r_q^{(G)} = R_q$
- 후보: $1 \le r_c^{(1)} < r_c^{(2)} < \dots < r_c^{(G)} = R_c$
g번째 그룹의 임베딩은 단순히 앞에서부터 잘라서 사용:
- $E^{(q,g)} = E^{(q)}_{meta}[1:r_q^{(g)},:]$
- $E^{(c,g)} = E^{(c)}_{meta}[1:r_c^{(g)},:]$
(2) 학습 : 모든 prefix 그룹을 “병렬로” 동시에 contrastive 학습
미니배치 B에 대해, 각 쿼리 $q^{(u)}$는
- positive $c^{(u)}$
- 추가 hard negative $c^{(u,-)}$
각 그룹 g마다 유사도 로짓은 온도 $\tau$로 스케일링:
\[S^{(g)}_{u,v} = \frac{1}{\tau} s^{(g)}(q^{(u)}, c^{(v)})\]InfoNCE는 (in-batch negatives + hard negative 포함)로 구성.
최종 손실:
\[L_{final} = \sum_{g=1}^{G} w_g L^{(g)}_{NCE}\]논문 설정에서는 $w_g=1$
3. 실험
3.1 실험 세팅
- 백본 VLM으로 Qwen2.5-VL / PaliGemma / Llama-3.2-Vision 등 다양한 구조 사용
- 평가:
- MMEB: 36개 태스크, Precision@1
- ViDoRe v2: 시각 문서 retrieval, 평균 NDCG@5
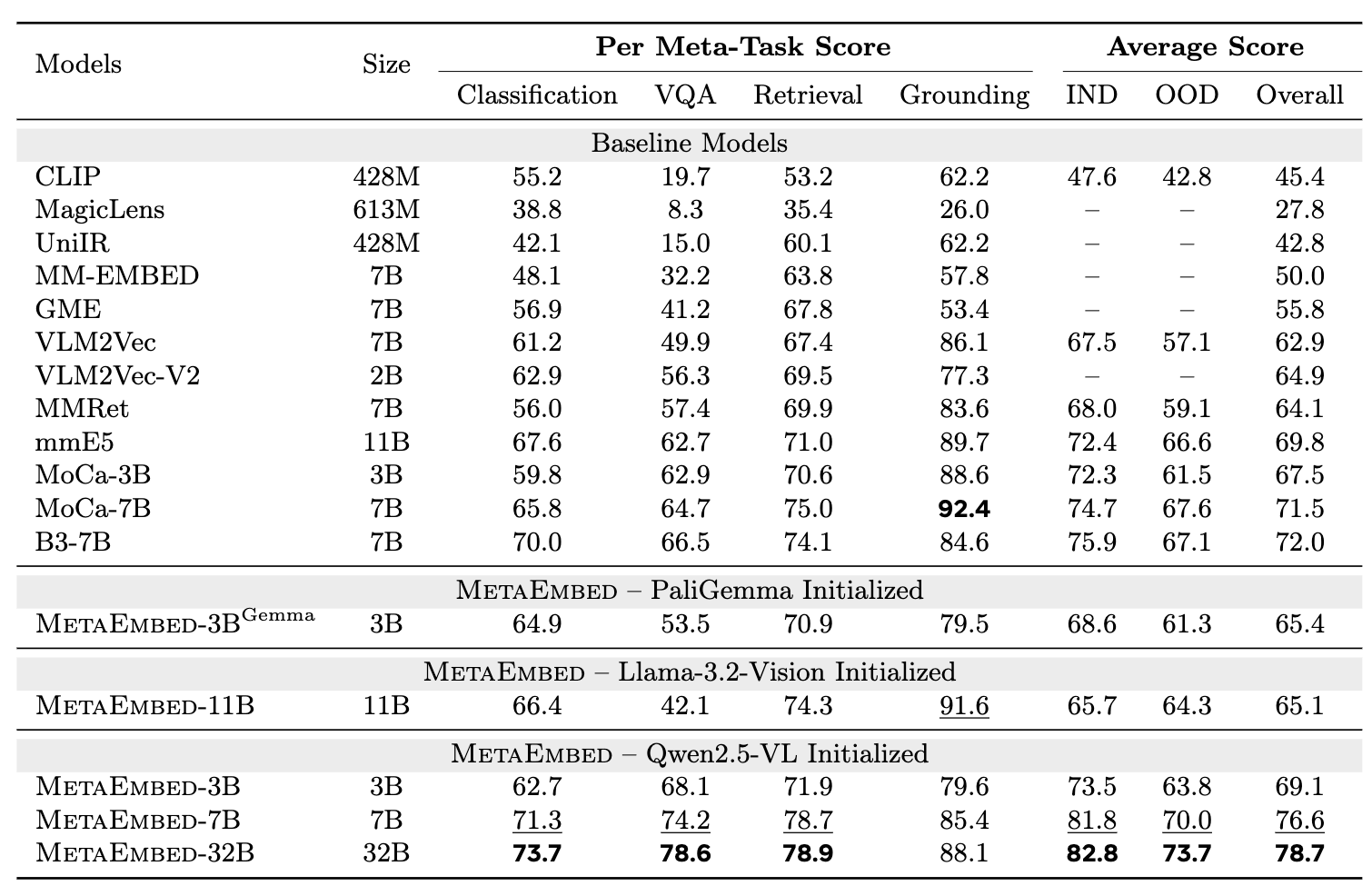
3.2 메인 결과
- MetaEmbed는 동일 또는 더 작은 모델 크기에서도
- single-vector 모델 대비 큰 폭의 성능 향상
- 기존 multi-vector 모델과 동급 또는 상회
- 7B → 32B 스케일 업 시 성능이 안정적으로 상승
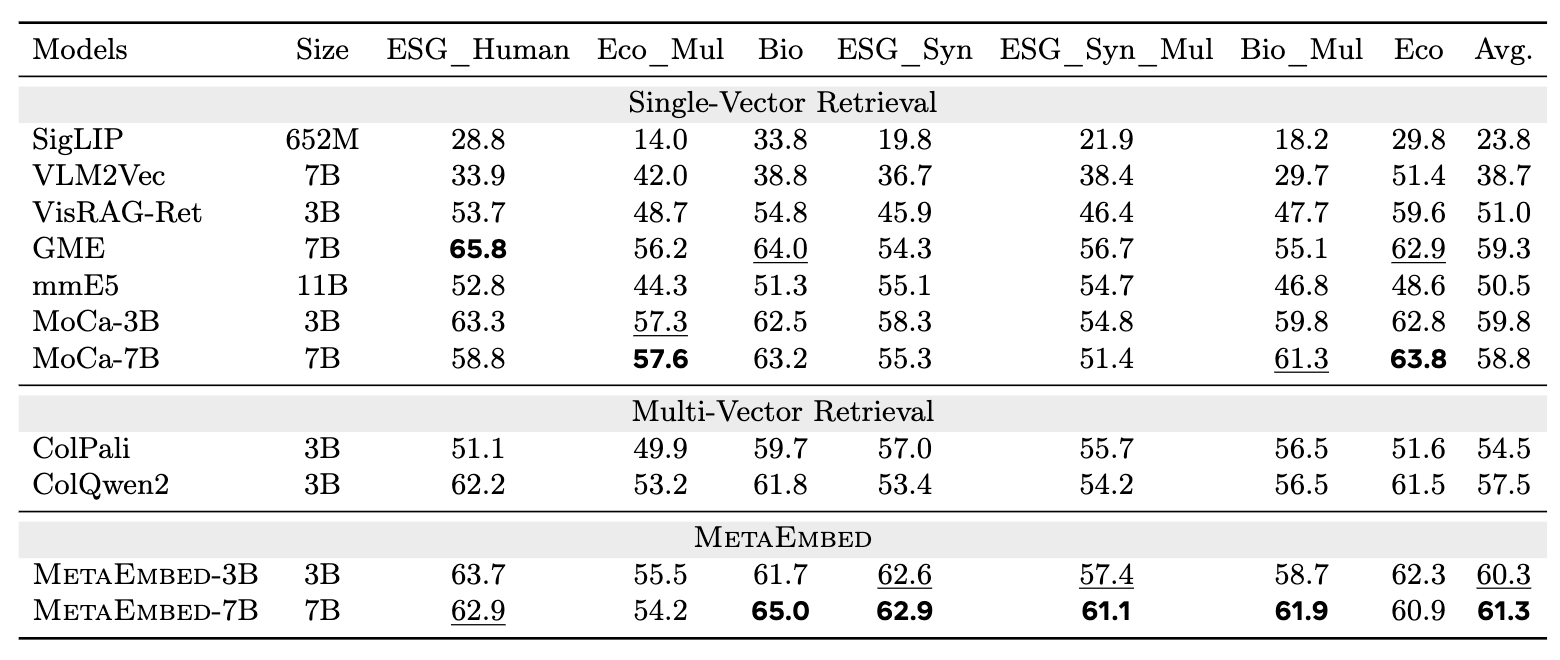
- MetaEmbed는
- 문서 구조/레이아웃이 중요한 환경에서도
- single-vector 대비 확실한 우위
- 기존 ColPali/ColQwen2 대비도 경쟁력 있는 성능
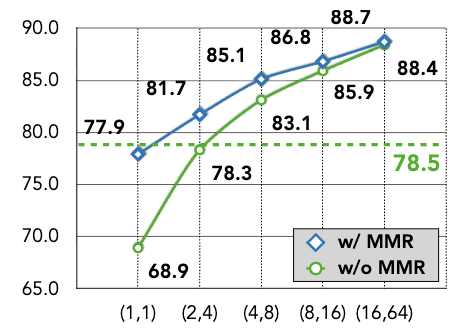
- 성능↑ ↔ 인덱스/비용↑ 트레이드오프를 정량화
- 대부분 예산 구간에서는 scoring이 compute bottleneck이 아니고, 오히려 쿼리 인코딩이 더 지배적 관찰
- Meta Tokens만으로는 부족
- prefix 구조를 학습 목표로 강제하는 MMR이 핵심 기여 요소
4. 결론
MetaEmbed는
- 학습 가능한 소수 Meta Tokens로 작지만 표현력 있는 멀티벡터를 만들고
- MMR(Matryoshka Multi-Vector Retrieval)로 그 벡터들을 coarse→fine prefix 구조로 정렬해
- 테스트 시점에 $(r_q, r_c)$ 를 선택함으로써 정확도·인덱스 크기·지연시간 사이를 유연하게 트레이드오프하는 “test-time scaling”을 가능하게 함