SMEC: Rethinking Matryoshka Representation Learning for Retrieval Embedding Compression

Written By. Biao Zhang, Lixin Chen, Tong Liu

배경 및 문제 정의

LLM은 문맥을 잘 이해하고 표현하기 위해 고차원 임베딩(예: 1024~4096 차원)을 생성하지만 아래와 같은 문제 존재:

• 저장 비용 증가
• 실시간 검색 시 연산량 급증
• 차원의 저주(Curse of Dimensionality)로 인한 검색 성능 저하

이러한 문제를 해결하기 위해 정적으로 차원을 선택해 사용할 수 있는 Matryoshka Representation Learning(MRL)이 제안되었지만 MRL은 앞 순서부터 선택한 차원을 자르는 정적인 indexing 방법을 사용하여 유연성 감소 및 각기 다른 차원에 대해 서로 다른 크기의 그래디언트가 적용되어 학습이 불안정함.

---

SMEC의 구성요소 3가지

SMEC는 세 가지 모듈로 구성:

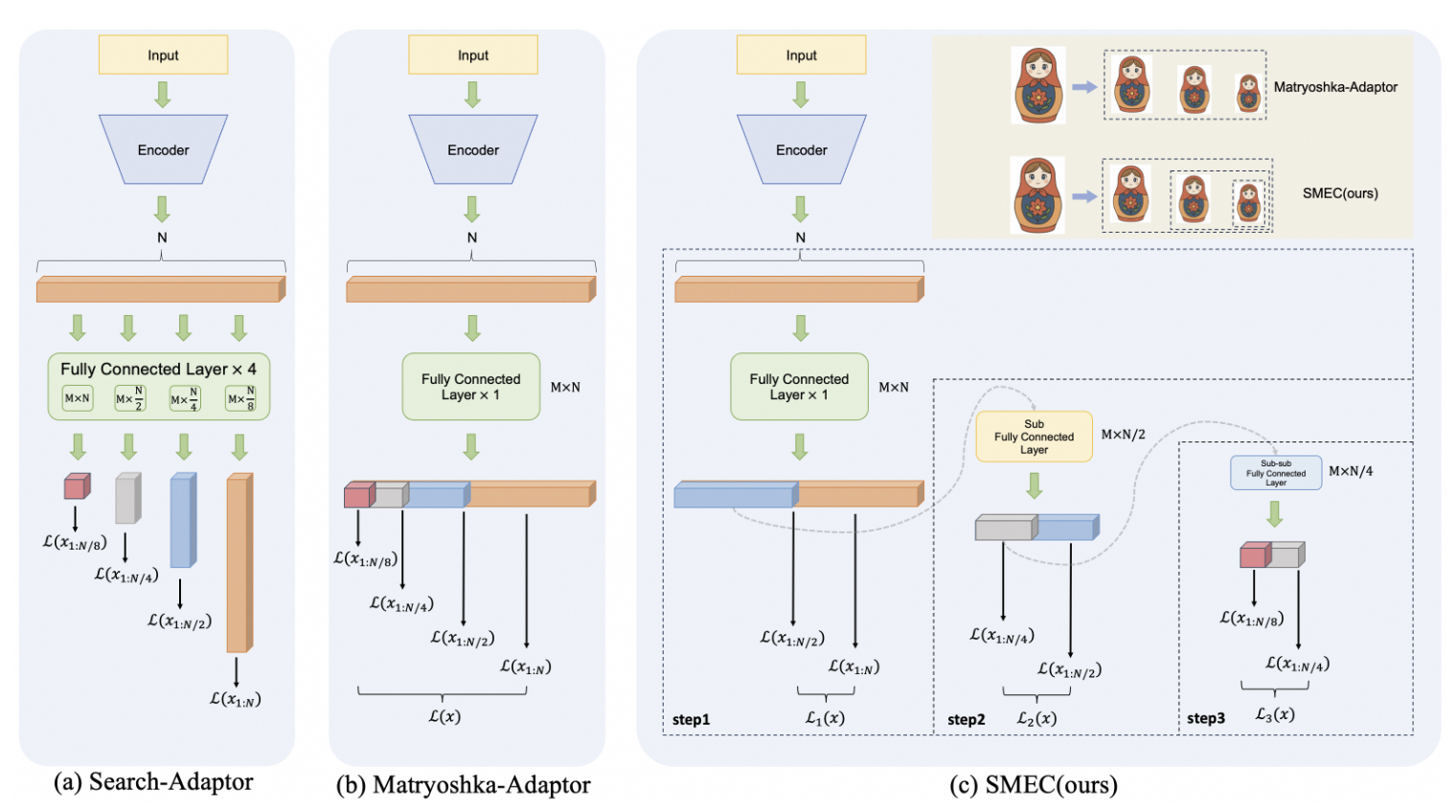
1. SMRL: Sequential Matryoshka Representation Learning
2. ADS: Adaptive Dimension Selection
3. S-XBM: Selectable Cross-Batch Memory

---

1. SMRL: Sequential Matryoshka Representation Learning

기존 MRL 문제점:

• 병렬적으로 여러 차원(D, D/2, D/4…)을 동시에 학습하면서 동일한 파라미터에 서로 다른 크기의 그래디언트가 적용됨
• 그로 인해 그래디언트 분산 증가 → 학습 불안정, 수렴 저하

SMRL 제안 방식:

• 차원 압축을 병렬이 아닌 순차적으로 수행하여 각 단계에서 그래디언트 분산을 줄이고 수렴을 가속화

• 논문에서는 그래디언트 분산 문제를 수식으로 다음과 같이 설명:

  \[\frac{\partial L_d}{\partial w_i} \propto \frac{1}{\delta(d)^2}\]
  • 여기서 $\delta(d)$는 차원 d에 따라 증가하는 함수로, 차원이 작아질수록 그래디언트가 커짐
    • 차원이 커질수록 norm이 커지므로 $\delta(d)$이 커짐
  • 결과적으로 낮은 차원에서의 손실이 파라미터에 지나치게 큰 영향을 주어 훈련이 불균형해짐

제안 해결책:

• Sequential 방식으로 차원 축소를 수행
• 각 단계에서는 직전 단계의 차원만 학습하며, 수렴 후에는 해당 파라미터를 freeze하여 다음 차원 학습 시 영향을 받지 않도록 함.

---

2. ADS: Adaptive Dimension Selection

기존 문제:

MRL은 고정된 차원(예: 상위 D/2 차원)을 단순히 자르기 때문에 중요한 정보를 잃을 수 있음

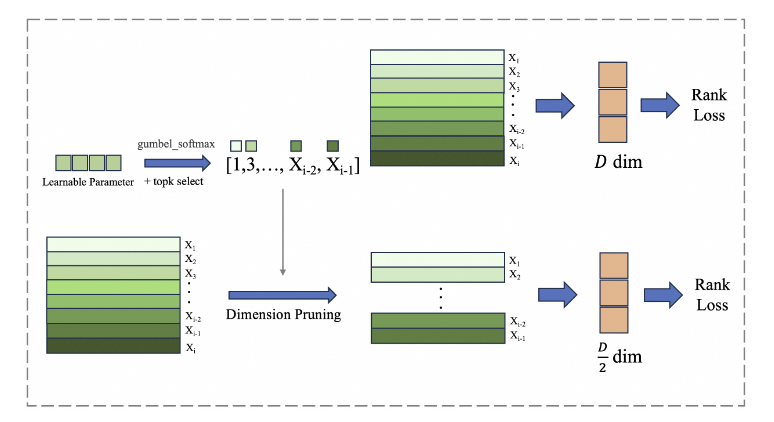
ADS 방식:

• 학습 중 차원의 중요도를 평가하고 가장 중요한 차원만 선택
• Gumbel-Softmax를 사용하여 확률적으로 차원을 선택 (gradient 가능)

• Gumbel noise $G \sim \text{Gumbel}(0, 1)$를 활용해 다음과 같이 표현:

  \[z = \text{softmax}_\tau(\hat{z} + G)\]
  • $\hat{z}$: 각 차원의 중요도 파라미터
• 결과적으로 확률적 샘플링 기반으로 임베딩 차원을 선택하게 됨

---

3. S-XBM: Selectable Cross-Batch Memory

기존 문제:

한 배치 안에서만 샘플링하면 다양성이 부족하고, noisy pairs가 생길 수 있음

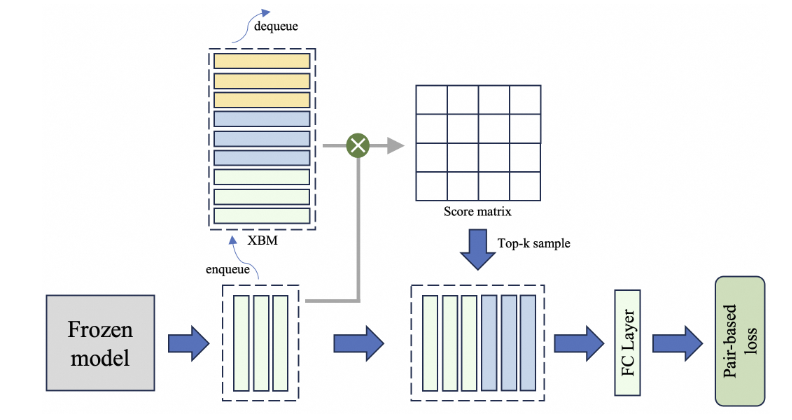
S-XBM 방식:

• 이전 배치의 임베딩을 메모리 큐에 저장 (FIFO)
• 현재 배치와 유사한 top-k 샘플만 선택하여 학습에 사용

• 손실 함수

  \[L_{\text{unsup}} = \sum_i \sum_{j \in NK(i)} \left| \text{Sim}(\text{emb}_i, \text{emb}_j) - \text{Sim}(\text{emb}_i[:d], \text{emb}_j[:d]) \right|\]
  • NK(i) : 메모리에서 유사도 top-k인 샘플들

---

4. SMEC 로스:

• 정답 쌍(j)이 오답 쌍(k)보다 더 유사하게 하도록 학습하는 rank 로스 사용

  \[L_{\text{rank}} = \sum_{i} \sum_{j} \sum_{k} \sum_{m} \mathbb{I}(y_{ij} > y_{ik}) (y_{ij} - y_{ik}) \cdot \log\left(1 + \exp(s_{ik}[:m] - s_{ij}[:m])\right)\]
  • 방식: pairwise margin-based ranking
  • $s_{ij}[:m]$ : 쿼리 i와 문서 j의 m-차원 임베딩 유사도, $\mathbb{I}(y_{ij} > y_{ik})$ : 정답 쌍인지 판별하는 indicator, $y_{ij} - y_{ik}$ : relevance score 차이 (크면 더 확실한 정답)

• 최종 학습 손실은 다음과 같이 정의:

  \[L_{\text{total}} = L_{\text{rank}} + \alpha \cdot L_{\text{unsup}}, \quad \alpha=0.1\]
  • 순위 기반 손실 + 비지도 학습 손실의 조합

---

실험 및 결과

사용된 데이터셋

• BEIR
  • 텍스트 기반 정보 검색 벤치마크
  • 13개 서브 데이터셋 포함 (Quora, FiQA, NFCorpus 등)
• Products-10K
  • 상품 이미지 검색 데이터셋
  • 약 10,000개 상품, 150,000개 이미지
• Fashion-200K
  • 이미지 ↔ 텍스트 크로스모달 검색
  • 약 200,000개 이미지-텍스트 쌍

---

실험 모델

• BEIR:
  • OpenAI text-embedding-3-large (3072D)
  • LLM2Vec (3548D, Qwen2-7B 기반)
• Products-10K / Fashion-200K:
  • LLM2CLIP

---

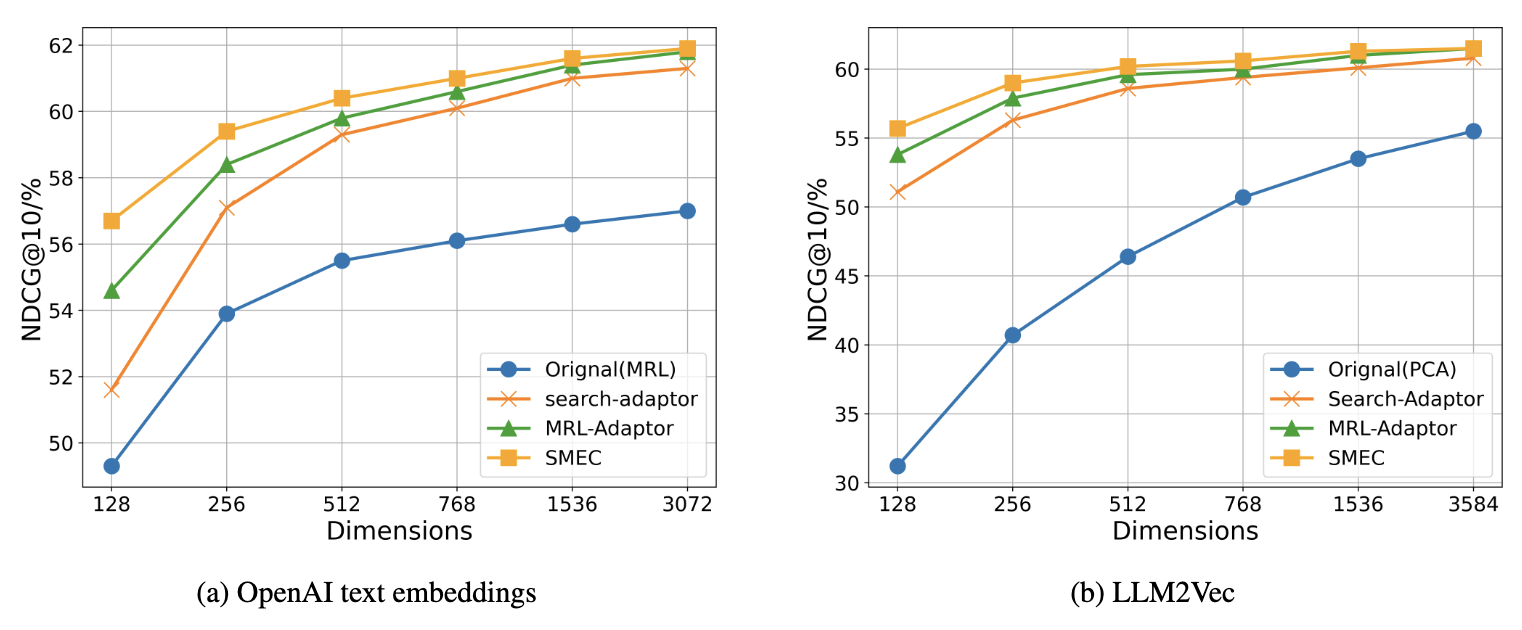
BEIR 실험 결과 (텍스트 검색)

• SMEC가 모든 압축 수준에서 가장 높은 nDCG@10 성능
• 특히 128차원 이하의 고압축 구간에서 성능 유지가 두드러짐

---

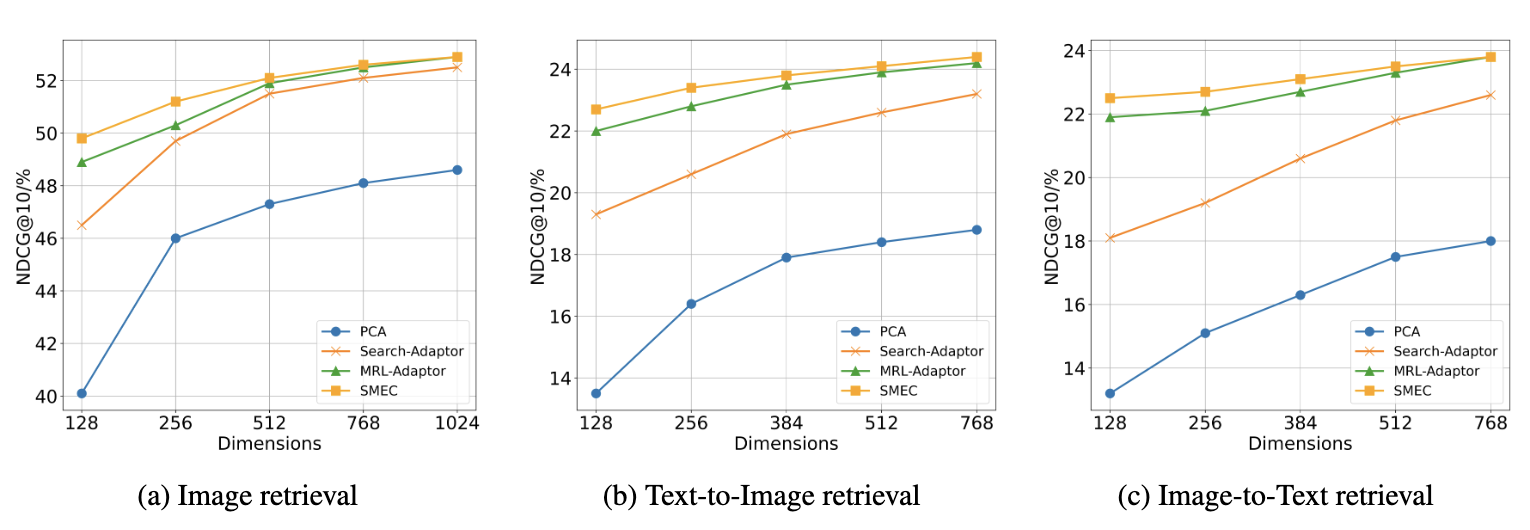
Products-10K (이미지 검색) & Fashion-200K 결과 (크로스모달 검색)

• 이미지 임베딩은 차원 감소 시 정보 손실이 큼 → ADS가 효과적
• Text → Image, Image → Text 모두에서 SMEC가 최고 성능
• SMEC는 다른 방법들보다 일관되게 높은 정확도 유지, 크로스모달에서도 압축 후 성능 저하가 적음

---

추가 실험 분석

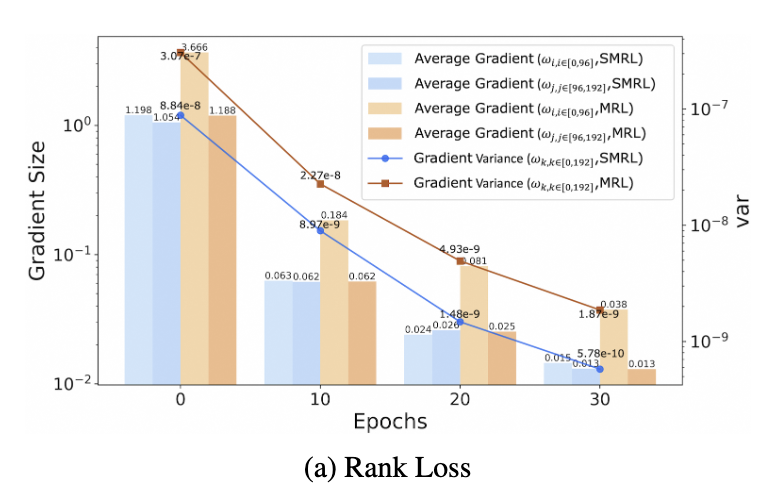
Gradient Variance 실험

• MRL은 학습 후반까지도 gradient variance가 큼 → 느린 수렴
• SMRL은 15 epoch부터 빠르게 수렴, 더 나은 성능 도달

---

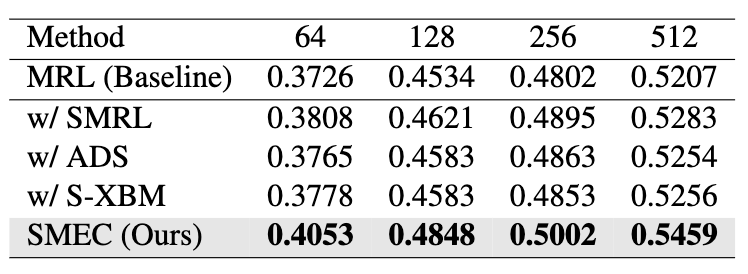
Ablation Study

• SMEC 구성요소를 하나씩 추가해가며 성능 향상 측정
• 가장 큰 기여는 SMRL → 그래디언트 안정화가 주요 요인
• ADS, S-XBM도 개별적으로 확실한 성능 향상 제공

---

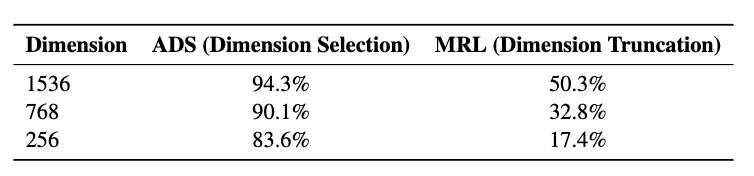
ADS의 효과 분석

• Achievement Rate of Important Dimension Selection (중요 차원 선택 달성률):
  • WARE (Weighted Average Reconstruction Error)라는 기준을 사용하여 각 차원의 중요도를 평가한 후, 실제로 선택된 차원들이 WARE 기준 상위 N개 중요한 차원 안에 얼마나 포함되는지를 비율로 나타낸 것

    • WARE : 특정 차원을 제거했을 때 모델의 출력(여기서는 임베딩 쌍 간의 유사도)이 얼마나 변하는지를 측정.

      \[WARE = \frac{1}{M} \sum_{m=1}^{M} \frac{|\hat{y}_m - y_m|}{|y_m|}\]
      • M: 샘플의 수, $\hat{y}_m$: m번째 샘플에 대한 차원 축소 전 모델의 점수(유사도), $y_m$: m번째 샘플에 대한 차원 축소 후 모델의 점수(유사도)

    • 즉, 이 달성률이 높을수록 해당 방법이 차원 축소 과정에서 중요한 정보를 더 잘 보존했음을 의미

• MRL은 단순 앞부분 자르기라 중요도 반영 못함
• ADS는 256D로 줄여도 중요 차원 83.6% 유지 → 정보 보존 효과 우수

---

S-XBM 메모리 사이즈 실험

• 메모리 큐 크기를 키울수록 정확도는 증가하지만 속도는 느려짐
• 5000 크기가 정확도와 학습속도 간 균형점으로 최적

결론

• 문제: LLM 기반 임베딩은 고차원이라 성능은 우수하지만 계산량 증가와 저장 부담으로 인해 실용성 떨어지고 이에 대한 해결책 중 하나인 MRL은 그래디언트가 불안정하고 차원 선택이 정적임.
• 제안: 이를 해결하기 위해, SMEC (Sequential Matryoshka Embedding Compression) 프레임워크를 도입
  • SMRL: 그래디언트 분산을 줄여 학습 안정화
  • ADS: 정보 손실 최소화를 위한 중요 차원 선택
  • S-XBM: 고차원-저차원 간 비지도 정렬 학습 강화
• 결과:
  • 다양한 도메인(텍스트, 이미지, 크로스모달)에서 고압축 상태에서도 성능 유지
  • 기존 기법 대비 우수한 정확도와 효율성